Route to Christmas: Day 20 2010

Today Route to Christmas takes another big step forward by introducing GPS analysis of today’s route – including a pace map and a calculation of the optimum route based on the GPS data. On top of that, the leg is also a nice one for you: A very long one from the Swedish Elitserien event of May 15th this year.

The leg is as usually first provided without routes – you may take a look at it and think about how you would attack this leg (if the image is too small, you may click on it to get it larger):

Webroute

Next you can draw your own route using the ‘Webroute’ below. Think through how you would attack this leg, and draw the route you would have made. Some comments about why you would choose a certain route are always nice for the other readers.

Then over to an analysis of the leg. With full GPS data of 20 runners instead of only Routegadget-data, it is possible to say a lot more about what is the best route than in the previous editions of Route to Christmas. The leg is maybe not the most interesting one as there are several routes which are approximately the same time, but still the following analysis gives some interesting information – and also shows how it is possible to analyze a leg using GPS data.

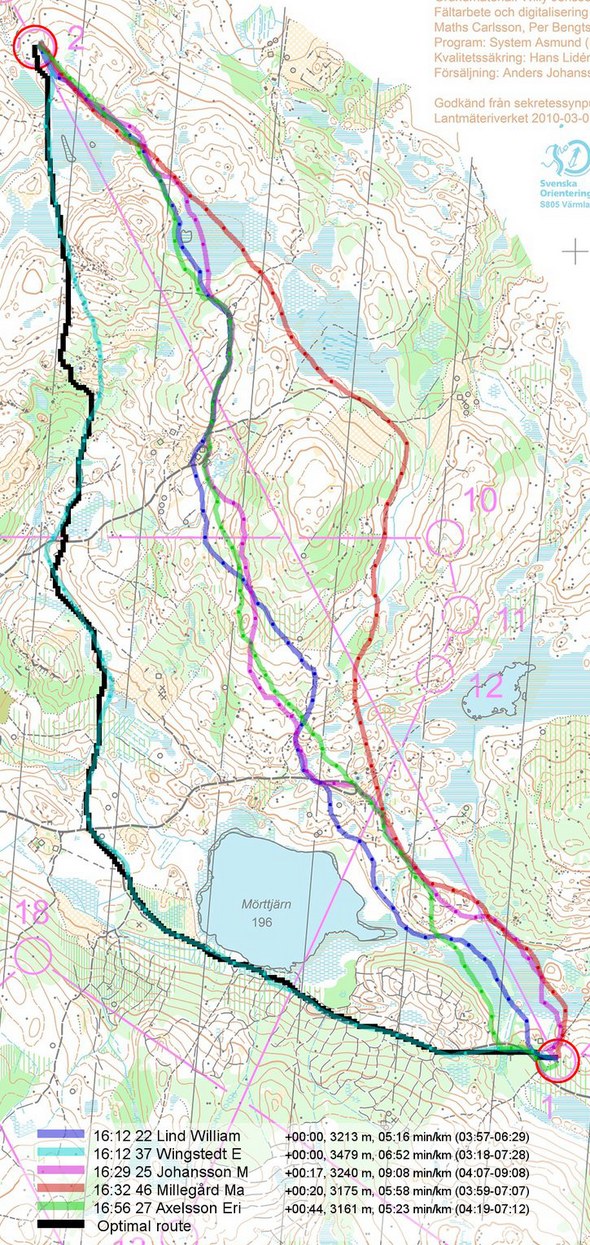
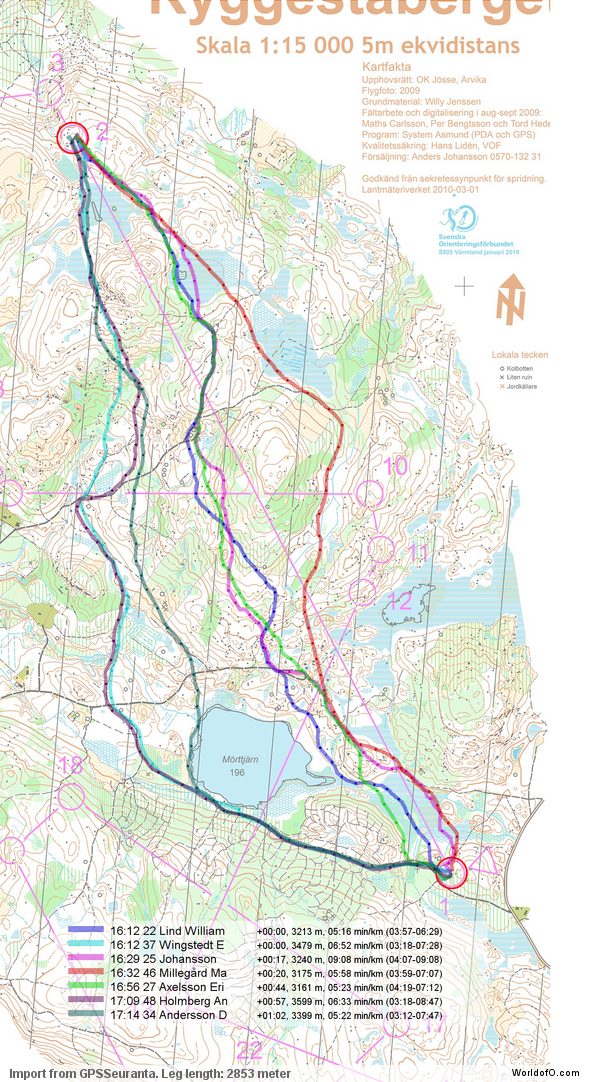
First we take a look at the routes of the fastest runners for the leg (note that the split times are based on the GPS data and not on the actual split times). As you can see from the routes, the direct variant and the left variant are approximately equal in time – whereas the right variant is somewhat slower based on the GPS data.

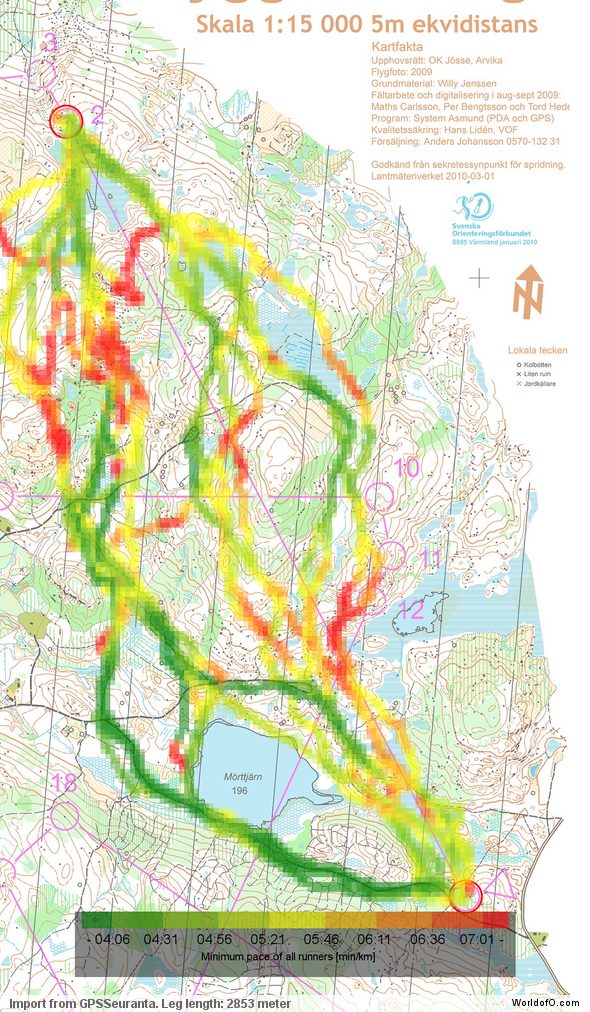
To get a better overview of all the possible choices for this leg – and how they relate to each other, we can plot each route with a color corresponding to the total time used for the leg (green is fast, red is slow). As you can see, there are a few green routes direct, a few left and one right. There slower options are also quite evenly distributed – with a few more on the left.

The next illustration is an interesting one. This illustration shows the minimum pace (in minutes/kilometers = maximum speed) for any given area on the leg on which one or more runners have been during the leg. Thus, if one runner has run in 5:00 min/km and another one on 6:00 min/km in an area, the area is given a color corresponding to 5:00 min/km. Thus all the green areas are the areas with good runnability and the red areas the ones with bad runnability. Following the left route along the left edge of the lake, you can see how the running speed is slower (towards yellow) at the south-west edge of the lake where the path is smaller and running through a marsh. One can also see how the speed is reduced in the light green / stony areas towards the end of the leg – and also the lower speed in the marshes.

We are still not finished with the analysis – now the fun part starts! With this speed map, we have actually got a lot of information which can be used to calculate the optimal route. Of course we have only got speed data for areas where a runner has been with a GPS during the leg, and therefore the calculated optimal route will have to go through areas where a runner has been. Below you see the calculated optimal route (in black) compared to the routes of the 5 fastest runners. As you can see, the calculate optimal route is a left variant – quite similar to the route of Emil Wingstedt for most of the leg. There are however some differences in some parts of the leg – this is because other runners have had a faster time for this part of the leg by choosing another micro-route-choice here. Thus for this particular case there are no big differences between the fastest route run by a runner and the calculated optimal route.

The algorithm for calculation of the optimal route (see more details below for the technically interested) gives some other interesting information: The fastest route to any point on the map which is reachable based on the speed information from the GPS data – and also the (relative) time it takes to get there. Thus, it is possible to make an illustration which gives information about why the optimal route is the optimal route. The illustration below is one way of displaying this information (please add a comment if you have a better idea – I have been trying many alternatives already and found that this was the best option so far). In this illustration, the starting point is set at the first control. Each position on the map is now colored based on how long it takes to reach it from the first control. Thus, all spots which it takes the same time to reach have the same color. Getting from the start to any of the dark red bands takes the same time. Correspondingly for the green, blue, yellow bands and so on. Note that the colors give the time it takes to get there, and says nothing about which way to get there. In addition to the color bands, the calculated optimal route is shown in black.

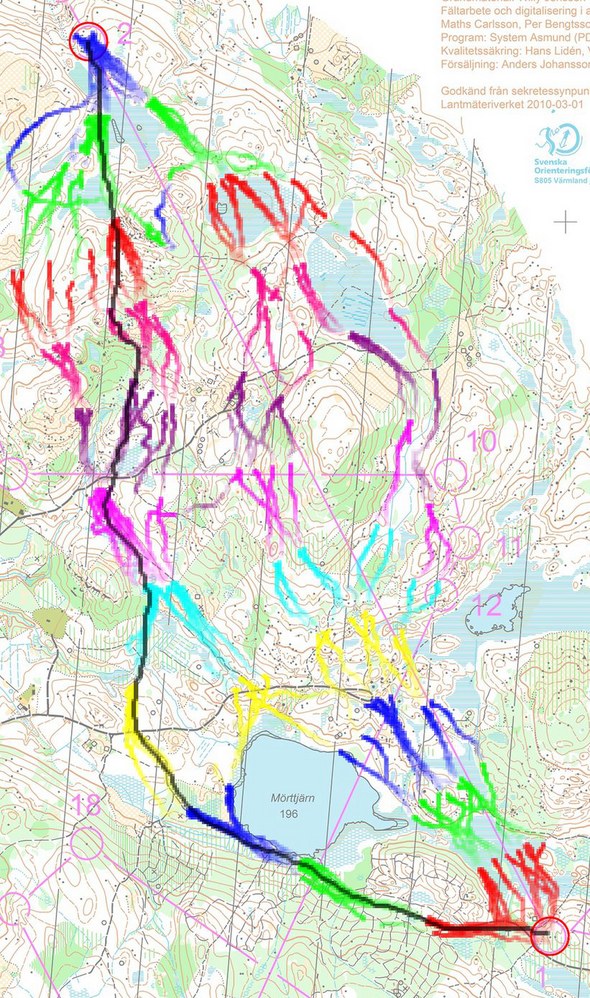
For some legs, this type of illustration can be used to find out where the control should have been placed in order to make another route be faster – this will be exemplified in a later edition of Route to Christmas. It can also be used to get an understanding about the dynamics of a leg – i.e. the difference between the different route choice options.

Technical background

A little bit of technical background about how there illustrations are made – more will come later on:

1. The leg is divided into a grid of around 1000×1000 (actually different grids have been used for some of the different illustrations above), and a speed is assigned to each grid cell based on the speed from the GPS data. I have worked both with average speed and maximum speed for each grid cell, and found that maximum gives the most correct results.
2. Using the speed data from this grid, I assigned the time it takes to get from any grid cell to an adjacent grid cell – either horizontally, vertically or diagonally. Based on this one can calculated the time it takes to get from any place to any other place on the grid.
3. Next I used Dijkstra’s algorithm to find the optimal path from the start control point to any other point in the grid by checking all the possible options (of course only using cells which have information about speed data – and only to/from cells where runners have been during the leg)
4. Using this data, it is easy to plot the optimal route from the start control point to the end control point. This optimal route is not necessarily equal to the best route by a runner, but rather takes different segments from different runners to find the best overall route.
5. Also using this data, it is possible to move the control a bit to either side, and see which route is the most optimal route for this control position (still only using the cells for which there is GPS data)
6. Finally I plotted all spots to which it takes the same time to arrive to in the same color. Note that there is no information in the illustration about which way you should go to get there, but it is mostly possible to see by following the color changes.
7. There are still a lot of interesting possibilities not explored here, but this type of analysis can surely be helpful in understanding the challenges and optimal routes in any terrain based on GPS data.
8. A possible extension would be to assign speed data to cells for which there is no GPS data – i.e. either extract data from an OCAD file or allow the user to “draw” pace in different areas to test different routechoice options. Actually, there is an article in the Scientific Journal of Orienteering doing a theoretical analysis of optimal route choice based on only calculated values for the speed based on OCAD data and altitude model.

There are probably not many of you reading all the way down here – but if you have come all the way down here, I would appreciate a comment about the usefulness of this kind of analysis! I have now got a setup which makes it possible to make these kind of analysis for hundreds of events with very little manual work – making it very interesting to explore this further!

Complete map in Omaps.worldofo.com

You find the complete map and Routegadget info in omaps.worldofo.com at this location.

Omaps.worldofo.com

The ‘Route to Christmas’ series at World of O was very popular the last years – and I’ve therefore decided to continue the series this Christmas as well. If you have got any good legs in RouteGadget from 2010-competitions – or old forgotten ones which are still interesting – please email me the link at Jan@Kocbach.net, and I’ll include it in Route to Christmas if it looks good. Route to Christmas will not be interesting if YOU don’t contribute.

There will be no analysis about the best routechoice for each leg – you can provide that yourself in the comments or in the Webroute. Not all legs are taken for the interesting routechoice alternatives – some are also taken because the map is interesting – or because it is not straightforward to see what to do on a certain leg. Any comments are welcome – especially if you ran the event chosen for todays leg!